Kinetic Energy And Work

KINETIC ENERGY

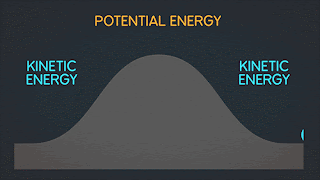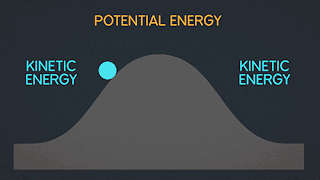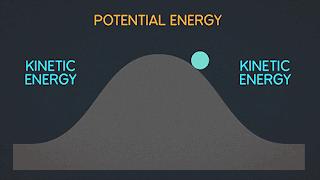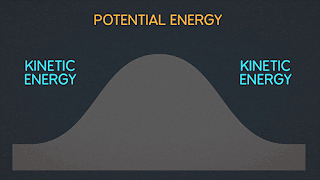
Kinetic Energy "K" is energy associated with the "state of motion" of an object. The faster the object moves the greater is its kinetic energy. When the object is stationary. Its kinetic energy is zero.

NOTE: 

^2=exponent number raised by the number two.

/  = is a division operator.

* = multiplication operator

Kinetic energy formula is K=1/2mv^2 

The SI unit of Kinetic energy (and all types of energy) is the joule (j) named for James Prescott Joule, an English scientist of the 1800's and defined as 1 joule = 1 J = 1 kg*m^2/s^2 





Example video on kinetic energy :

WORK

Work W is energy transferred to or from an object by means of a force acting on the object. Energy transferred to the object is positive work and energy transferred from the object is negative work

Work have an three sub topics include  forces and displacement they are:

Work done by  gravitational force 
Work done by  spring force

Work done by a variable force.

NOTE:

The formula of the work is W=F*D

Where F=magnitude of applied force and D= displacement of the object 
we see that work= force * distance


Example of work is : if you push the box with the constant force of 100N over the 10m distance you would do 1,000N.m of work these and that is equal to 1,000joules. 

• work is only done when displacement occur.
• if you push a brick of wall that as the same the matter of box you may get very tired but technically you will done zero work.
• because no displacement is equal to zero work.

• work is positive if the applied force is in the same direction as the displacement.
• work is negative  if the applied force is in the direction opposite the displacement.

• the sign of work is very important because it's tell us the speed of an object whether it will increase or decrease as the result of applying the work.

work done  by the gravitational forces: 

If you apply a force on a moving object, we say that the force you are exerting performs a work. 
The work will be proportional to the magnitude of the force exerted by the distance traveled. Gravitational force is defined as the force that attracts a body to the earth or to any other physical body that has mass. If the body moves under the action of the gravitational force, it also performs a work called gravitational work. If a particular object is falling, the particle is forced to point in the direction of gravity. The magnitude of the fall of the body depends on the mass, the gravitational constant and the height from which it is falling.

In my discussion at work we already know that  the equation  of work is  

work = force * distance 

and when gravitational  is occur  the equation   of  gravitational force is 

force = mass * gravity  

And if we include the gravitational force and work the equation will be.

work = mass * gravity * distance  or work = mass * gravity * height 

because we consider that the change of distance in terms of y - axis  

Example :


A pencil falls from a table. It calculates the work done by the force of gravity. Consider that the mass of the pencil is 10 grams and the height of the table is 60 cm.


answer:

The pencil falls under the action of the force of gravity, to calculate the work done, therefore we will use the equation above, where m = 10 g = 0.01 kg, g = 9.8 m/s^2, h = 60 cm = 0.6 m.

W = 0.01 kg* 9.8 m/s^2 * 0.6 m
W = 0.06 J.

Work done by spring force

Spring is an arrangement, which is capable to apply force on a body. As we will see, spring force is similar to gravity in many important ways. At the same time, it is different to gravity in one important way that it applies a variable force unlike gravity.

Spring force is given by the expression : F=−kx

where k is spring constant, measured experimentally for a particular spring. The value of k (=-F/x) measures the stiffness of the spring. A high value indicates that we would require to apply greater force to change length of the spring.

Now, we are set to obtain an expression for the work done by the spring.

Let the extension of the spring be “x”. Then,   F=−kx

As the force is variable, we can not use the expression “Frcosθ” to determine work. It is valid for constant force only. We need to apply expression, involving integration to determine work :

where: Ws = ∫F(x)dx

Let xi and xf be the initial and final position of the block with respect to origin then 

Ws = ∫xi to xf - kx ix

Ws= -k[x^2/2] xi to xf

Ws = 1/2 k (xi^2 - xf^2)

If block is at origin then xi = 0 and xf  = x (say) then the equation os Ws = -1/2 kx^2

Example problem 

Problem : A block of 1 kg is attached to the spring and is placed horizontally with one end fixed. If spring constant is 500 N/m, find the work done by the horizontal force to pull the spring slowly through an extension of 10 cm.

Solution : Though, it is not explicitly stated, but it can be inferred from the word "slowly" that the block is pulled without any kinetic energy. This is a situation, when initial and final speeds are zero. This means that initial and final kinetic energies are zero (equal). Hence, work done by the two forces (external applied force and spring force) is zero. In this condition, work done by the horizontal force is equal to the work done by the spring force, but opposite in sign. Now work done by the spring force is :

WS=−12*500x*0.01^2

WS= - 2.5 J

Work done by the horizontal force is:

Ws= 2.5 j 

Work done by variable force:

• So far we have defined work done by a Force which is constant in both magnitude and direction.
• However, work can be done by forces that varies in magnitude and direction during the displacement of the body on which it acts.
• For simplicity consider the direction of force acting on the body to be along x-axis also consider the force F(x) is some known function of position x

Example work done by variable force

A force F = 2x + 5 acts on a particle. Find the work done by the force during the displacement of the particle from x =0m to x = 2m. Given that the force is in Newtons.

Work done W = ∫F(x)dx

Thus W = = ∫F(x)dx Cos 0o

= ∫F(x)dx

= ∫(2x + 5)dx

= 2x2/2 + 5x |

= 22 + 5 x 2

= 14 J

POWER IN TERMS OF WORK

Power

The time rate at which work is done by a force is said to be the power due to the

force. If a force does an amount of work W in an amount of time %t, the average

power due to the force during that time interval is = Paverage=W/∆T 

POWER ALSO  is a rate at which work is done, or energy is used. It is equal to the amount of work done divided by the time it takes to do the work. The unit of power is the Watt (W), which is equal to a Joule per second (J/s).

The instantaneous power P is the instantaneous time rate of doing work, which

we can write as P=dW/dt

NOTE:

the equation of power in terms of work is P= ∆ W / ∆ T

EXAMPLE OF POWER IN TERMS OF WORK:

How much energy is used by a 60-Watt light bulb that has been left on for eight hours?

Answer: The power of the light bulb is given, as well as a time interval. The time is 8 hours, or (8 hours)(60 minutes/hour)(60 seconds/minute) = 28800 s. The energy used can be found by rearranging the equation:

 P= ∆W/∆T then ∆W = P* ∆T

∆W = P∙∆t

∆W = (60 W)∙(28800 s)

∆W = 1728000 J

∆W = 1728 kJ

The energy expended by the 60-Watt light bulb in 8 hours was 1728000 J, or 1728 kJ.

short quiz 

1.Determine the kinetic energy of a 625-kg roller coaster car that is moving with a speed of 18.3 m/s.

Answer:KE = 1.05 x10^5 Joules

2. If the roller coaster car in the above problem were moving with twice the speed, then what would be its new kinetic energy?

Answer: KE = 4.19 x 10^5 Joules

3.Missy Diwater, the former platform diver for the Ringling Brother's Circus, had a kinetic energy of 12 000 J just prior to hitting the bucket of water. If Missy's mass is 40 kg, then what is her speed?

Answer: v = 24.5 m/s

4. A 900-kg compact car moving at 60 mi/hr has approximately 320 000 Joules of kinetic energy. Estimate its new kinetic energy if it is moving at 30 mi/hr.

Answer: KE = 80 000 J

5.A car is traveling at a velocity of 10 m/s and is has a mass of 250 Kg. Compute its Kinetic energy? 

Answer:KE = 12500 kgm^2 s^2

6.A man is transporting a trolley of mass 6 Kg and having Kinetic energy of 40 J. Compute its Velocity with which he is running?

Answer: v = 3.65m/s

7.What is the Kinetic Energy of a 150 kg object that is moving with a speed of 15 m/s?

Answer: KE = 16875J

8.An object has a kinetic energy of 25 J and a mass of 34 kg , how fast is the object moving? 

Answer: v = 1.28m/s 

9.A box is dragged across a floor by a 100N force directed 60o above the horizontal. How much work does the force do in pulling the object 8m?

Answer: m = 400 J

10: A box is dragged horizontally across a floor by a 100 N force acting parallel to the floor. What is the work done by the force in moving it through a distance of 8 m. 

Answer: 800 J

REFERENCES:

https://www.toppr.com/guides/physics/work-energy-and-power/work-and-kinetic-energy/

https://opentextbc.ca/physicstestbook2/chapter/kinetic-energy-and-the-work-energy-theorem/

https://www.khanacademy.org/science/ap-physics-1/ap-work-and-energy/kinetic-energy-ap/a/what-is-kinetic-energy

http://teacher.pas.rochester.edu/phy121/lecturenotes/Chapter07/Chapter7.html

https://courses.lumenlearning.com/boundless-physics/chapter/work-energy-theorem/

http://spiff.rit.edu/classes/phys311.old/lectures/kinework/kinework.html

https://physics.stackexchange.com/questions/337781/relation-and-difference-between-work-and-kinetic-energy

wawswh